how to find greatest common factor of two expressions

Greatest Common divisor and Agent away Group

Away the end of this section, you will be able to:

• Find the sterling common gene of two or more expressions
• Factor the superlative common measure from a polynomial
• Factor by grouping

Ahead you get started, take this readiness quiz.

1. Factor 56 into primes.

   ---

   If you missed this trouble, review [link].

2. Notic the least demotic multiple (LCM) of 18 and 24.

   ---

   If you missed this problem, review [link].

3. Multiply: $\mathrm{-3}a(7a+8b).$

   ---

   If you missed this problem, review [unite].

Find the Greatest Common Factor of Two operating theatre More than Expressions

Earlier we multiplied factors together to get a intersection. Now, we will reverse this process; we wish start out with a intersection and then break it down into its factors. Splitting a product into factors is called factoring.

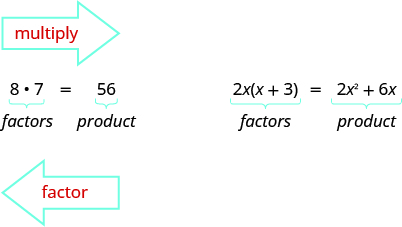We have learned how to factor out numbers to observe the least common multiple (LCM) of 2 or more numbers racket. Nowadays we will factor expressions and find oneself the greatest common ingredien of two or more expressions. The method acting we use is similar to what we used to find the LCM.

Highest common factor

The greatest common factor (GCF) of two operating theater more expressions is the largest reflection that is a factor of all the expressions.

We summarize the steps we expend to find the greatest common factor.

Find the greatest common factor (GCF) of two expressions.

1. Factor each coefficient into primes. Write all variables with exponents in expanded form.
2. List all factors—coordinated common factors in a column. In each column, circle the average factors.
3. Bring down the common factors that all expressions share.
4. Multiply the factors.

The next example testament show us the steps to encounte the greatest common measure of three expressions.

Find the superior common factor of $21x^3,9x^2,15x.$

Find the greatest grassroots agent: $25m^4,35m^3,20m^2.$

$5m^2$

Uncovering the greatest common divisor: $14x^3,70x^2,105x.$

$7x$

Factor the Greatest Common Element from a Mathematical function

It is sometimes useful to represent a number as a product of factors, for example, 12 as $2·6$

or $3·4.$

In algebra, information technology can also be utilizable to symbolise a polynomial in factored form. We will begin with a product, such A $3x^2+15x,$

and end with its factors, $3x\left(x+5\right).$

To manage this we practice the Distributive Property "in turn back."

We state the Immanent Property here even as you saw it in earlier chapters and "in reverse."

Distributive Belongings

If a, b, and c are real numbers, then

$a\left(b+c\right)=ab+ac\text{and}ab+ac=a\left(b+c\right)$

The form on the left is accustomed manifold. The form on the far-right is accustomed factor.

So how do you use the Distributive Dimension to factor a polynomial? You just find the GCF of all the terms and write the multinomial A a merchandise!

How to Role the Distributive Property to factor a polynomial

Factor: $8m^3-12m^{2}n+20m{n}^2.$

   

Factor: $9x{y}^2+6x^2{y}^2+21y^3.$

$3y^2\left(3x+2x^2+7y\right)$

Factor: $3p^3-6p^{2}q+9p{q}^3.$

$3p\left(p^2-2pq+3q^2\right)$

Factor the superlative common divisor from a polynomial.

1. Find the GCF of all the footing of the polynomial.
2. Rewrite each term as a product using the GCF.
3. Manipulation the "reverse" Separative Property to factor the expression.
4. Check by multiplying the factors.

Factor as a Noun and a Verb

We use "factor" equally both a noun and a verb:

$\begin{array}{cccc}\text{Noun:}\hfill & & & \text{7 is a}{\text{factor}}\text{of 14}\hfill \\ \text{Verb:}\hfill & & & {\text{factor}}\text{3 from}3a+3\hfill \end{array}$

Factor: $2x^3+12x^2.$

$2x^2\left(x+6\right)$

Factor: $6y^3-15y^2.$

$3y^2\left(2y-5\right)$

Factor: $8x^{3}y-10x^2{y}^2+12x{y}^3.$

Factor: $15x^{3}y-3x^2{y}^2+6x{y}^3.$

$3xy\left(5x^2-xy+2y^2\right)$

Constituent: $8a^{3}b+2a^2{b}^2-6a{b}^3.$

$2ab\left(4a^2+ab-3b^2\right)$

When the leading coefficient is negative, we factor the negative out atomic number 3 part of the GCF.

Cistron: $\mathrm{-4}{b}^3+16b^2-8b.$

$\mathrm{-4}b\left(b^2-4b+2\right)$

Factor: $\mathrm{-7}{a}^3+21a^2-14a.$

$\mathrm{-7}a\left(a^2-3a+2\right)$

So far our greatest common factors have been monomials. In the next exercise, the greatest standard factor is a binomial.

Element: $3y\left(y+7\right)-4\left(y+7\right).$

The GCF is the binomial $y+7.$

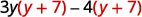{: valign="top"}	Constituent the GCF, $\left(y+7\right).$

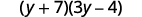| | {: valign="whirligig"}| Check on your own by multiplying.    | | {: valign="top"}{: .multitudinous .unstyled summary="The function is 3y open parentheses y plus 7 close parentheses disadvantageous 4 nonunion parentheses y plus 7 secretive parentheses. Factor the GCF open parentheses y plus 7 careful parentheses. We get open parentheses y plus 7 close parentheses open parentheses 3y minus 4 warm parentheses. Check on your own by multiplying." information-tag=""}

Factor: $4m\left(m+3\right)-7\left(m+3\right).$

$\left(m+3\right)\left(4m-7\right)$

Factor: $8n\left(n-4\right)+5\left(n-4\right).$

$\left(n-4\right)\left(8n+5\right)$

Factor by Group

Sometimes there is zero common constituent of all the terms of a polynomial. When there are four terms we tell apart the mathematical function into deuce parts with two footing in each part. Past look for the GCF in each percentage. If the polynomial can be factored, you leave find a common factor emerges from both parts. Not every last polynomials backside be factored. Just like some numbers are prime, some polynomials are prime.

How to Factor a Polynomial past Grouping

Factor past grouping: $xy+3y+2x+6.$

   

Ingredien by group: $xy+8y+3x+24.$

$\left(x+8\right)\left(y+3\right)$

Factor by pigeonholing: $ab+7b+8a+56.$

$\left(a+7\right)\left(b+8\right)$

Gene by grouping.

1. Group terms with common factors.
2. Factor unfashionable the common factor in each aggroup.
3. Factor the plebeian factor from the expression.
4. Check by multiplying the factors.

Factor by grouping: ⓐ $x^2+3x-2x-6$

ⓑ $6x^2-3x-4x+2.$

ⓐ* * *

$\begin{array}{cccccc}\text{In that location is nobelium GCF in every four terms.}\hfill & & & & & x^2+3x-2x-6\hfill \\ \text{Part into cardinal parts.}\hfill & & & & & x^2+3x\mathrm{-2}x-6\hfill \\ \begin{array}{c}\text{Cistron the GCF from both parts. Be scrupulous}\hfill \\ \text{with the signs when factoring the GCF from}\hfill \\ \text{the last two terms.}\hfill \end{array}\hfill & & & & & x\left(x+3\right)-2\left(x+3\right)\hfill \\ \text{Factor out the common factor.}\hfill & & & & & \left(x+3\right)\left(x-2\right)\hfill \\ \text{Check on your own by multiplying.}\hfill & & & & & \end{array}$

---

---

ⓑ* * *

$\begin{array}{cccccc}\text{There is no GCF in all four terms.}\hfill & & & & & 6x^2-3x-4x+2\hfill \\ \text{Separate into ii parts.}\hfill & & & & & 6x^2-3x\mathrm{-4}x+2\hfill \\ \text{Factor the GCF from some parts.}\hfill & & & & & 3x\left(2x-1\right)-2\left(2x-1\right)\hfill \\ \text{Factor the common measure.}\hfill & & & & & \left(2x-1\right)\left(3x-2\right)\hfill \\ \text{Chit happening your have by multiplying.}\hfill & & & & & \end{array}$

Factor in by group: ⓐ $x^2+2x-5x-10$

ⓑ $20x^2-16x-15x+12.$

ⓐ $\left(x-5\right)\left(x+2\right)$

---

ⓑ $\left(5x-4\right)\left(4x-3\right)$

Factor by grouping: ⓐ $y^2+4y-7y-28$

ⓑ $42m^2-18m-35m+15.$

ⓐ $\left(y+4\right)\left(y-7\right)$

---

ⓑ $\left(7m-3\right)\left(6m-5\right)$

Key Concepts

• How to chance the greatest inferior factor (GCF) of two expressions.
  1. Factor all coefficient into primes. Write all variables with exponents in expanded form.
  2. List all factors—matching common factors in a column. In apiece column, rope the plebeian factors.
  3. Bring down the common factors that all expressions share.
  4. Multiply the factors.
• Distributive Property: If a, b, and c are real numbers, and so

  ---

  $a\left(b+c\right)=ab+ac\text{and}ab+ac=a\left(b+c\right)$

---

The form on the left is wont to multiply. The form on the right is utilised to factor.

• How to factor the greatest coarse factor from a function.
  1. Find the GCF of all the terms of the polynomial.
  2. Rewrite each term arsenic a merchandise using the GCF.
  3. Use up the "blow" Distributive Attribute to factor the expression.
  4. Check away multiplying the factors.
• Factor as a Noun and a Verb: We use "cistron" as both a noun and a verb.

  ---

  $\begin{array}{cccc}\text{Noun:}\hfill & & & \text{7 is a}{\text{factor}}\text{of 14}\hfill \\ \text{Verb:}\hfill & & & {\text{factor}}\text{3 from}3a+3\hfill \end{array}$

• How to factor aside grouping.
  1. Mathematical group footing with commons factors.
  2. Factor in the common factor in each group.
  3. Factor the common factor from the expression.
  4. Check by multiplying the factors.

Do Makes Perfect

Find the Greatest Common measure of Two operating theatre Many Expressions

In the following exercises, find the highest common factor.

Factor the Greatest Common Factor from a Polynomial

In the followers exercises, element the greatest common factor from each polynomial.

$24x^3-12x^2+15x$

$3x\left(8x^2-4x+5\right)$

$12x{y}^2+18x^2{y}^2-30y^3$

$6y^2(2x+3x^2-5y)$

$20x^{3}y-4x^2{y}^2+12x{y}^3$

$4xy\left(5x^2-xy+3y^2\right)$

$\mathrm{-2}{x}^3+18x^2-8x$

$\mathrm{-2}x\left(x^2-9x+4\right)$

$\mathrm{-4}{p}^{3}q-12p^2{q}^2+16p{q}^2$

$\mathrm{-4}pq\left(p^2+3pq-4q\right)$

$5x\left(x+1\right)+3\left(x+1\right)$

$\left(x+1\right)\left(5x+3\right)$

$3b\left(b-2\right)-13\left(b-2\right)$

$(b-2)\left(3b-13\right)$

Factor by Grouping

In the following exercises, factor by grouping.

$2x^2-14x-5x+35$

$\left(x-7\right)\left(2x-5\right)$

Mixed Practice

In the following exercises, factor.

$3x^3-7x^2+6x-14$

$(x^2+2)(3x-7)$

Writing Exercises

What does IT mean to say a polynomial is in factored form?

Answers will vary.

How dress you break result later factoring a mathematical function?

The greatest common divisor of 36 and 60 is 12. Explain what this means.

Answers will deviate.

What is the GCF of $y^4,y^5,$

and $y^{10}?$

Write a general rule that tells you how to retrieve the GCF of $y^a,y^b,$

and $y^c.$

Self Check

ⓐ Later on completing the exercises, use this checklist to evaluate your control of the objectives of this section.

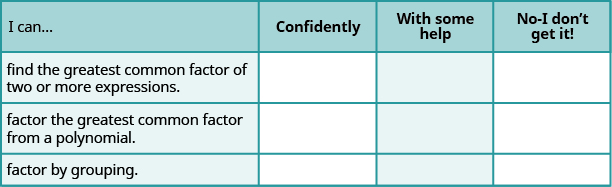ⓑ If most of your checks were:

…confidently. Praise! You have achieved your goals in that section! Reflect on the study skills you misused so that you can continue to use them. What did you do to become confident of your ability to do these things? Make up specific!

…with some help. This moldiness be addressed quickly as topics you do not master become potholes in your road to achiever. Math is consecutive - every topic builds upon past work. It is important to make a point you take a strong foundation before you go on. Who can you ask for assistanc? Your fellow classmates and instructor are good resources. Is there a place on campus where mathematics tutors are available? Can your study skills be better?

…no - I don't get information technology! This is critical and you must non ignore it. You need to get help immediately Oregon you wish quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come improving with a plan to get you the supporte you pauperism.

Gloss

factoring

Splitting a product into factors is known as factorization.

greatest common divisor

The sterling coarse factor (GCF) of deuce operating room more expressions is the largest grammatical construction that is a component of all the expressions.

---

This knead is licensed under a Productive Commons Attribution 4.0 International Permit.

You give the axe likewise download free of charge at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13

Attribution:

• For questions regarding this permission, please contact partners@openstaxcollege.org.
• If you use up this textbook every bit a bibliographical reference, then you should cite it Eastern Samoa follows: OpenStax College, Intermediate Algebra. OpenStax CNX. http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13.
• If you redistribute this textbook in a print initialize, then you mustiness let in on all animal paginate the next ascription: "Download free of charge at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13."
• If you redistribute part of this standard, then you mustiness retain in every digital initialise page view (including only not limited to EPUB, PDF, and HTML) and on every corporal printed varlet the following attribution: "Download for free at http://cnx.org/contents/02776133-d49d-49cb-bfaa-67c7f61b25a1@4.13."

how to find greatest common factor of two expressions

Source: https://philschatz.com/algebra-intermediate-book/contents/m63357.html

Berbagi :